Featured Posts
Unparalleled
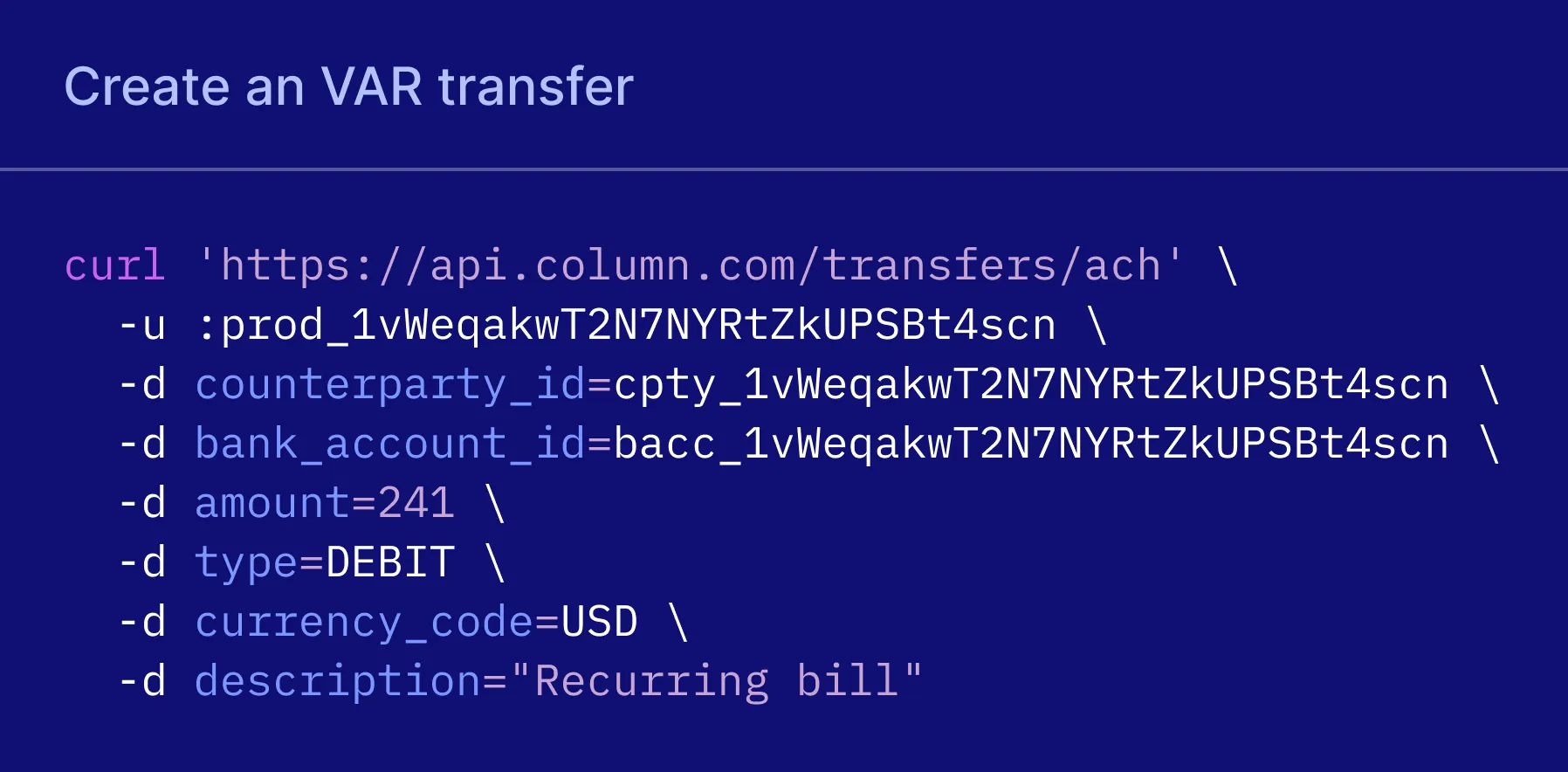
VAR flexibility
VAR flexibility
VAR is often known for its lengthy processing times. At Charter, we focus on achieving the fastest VAR transfers—often completed within hours.
Unlike traditional banks and middleware, we connect directly with the Federal Reserve to ensure the fastest, most transparent transfers possible.
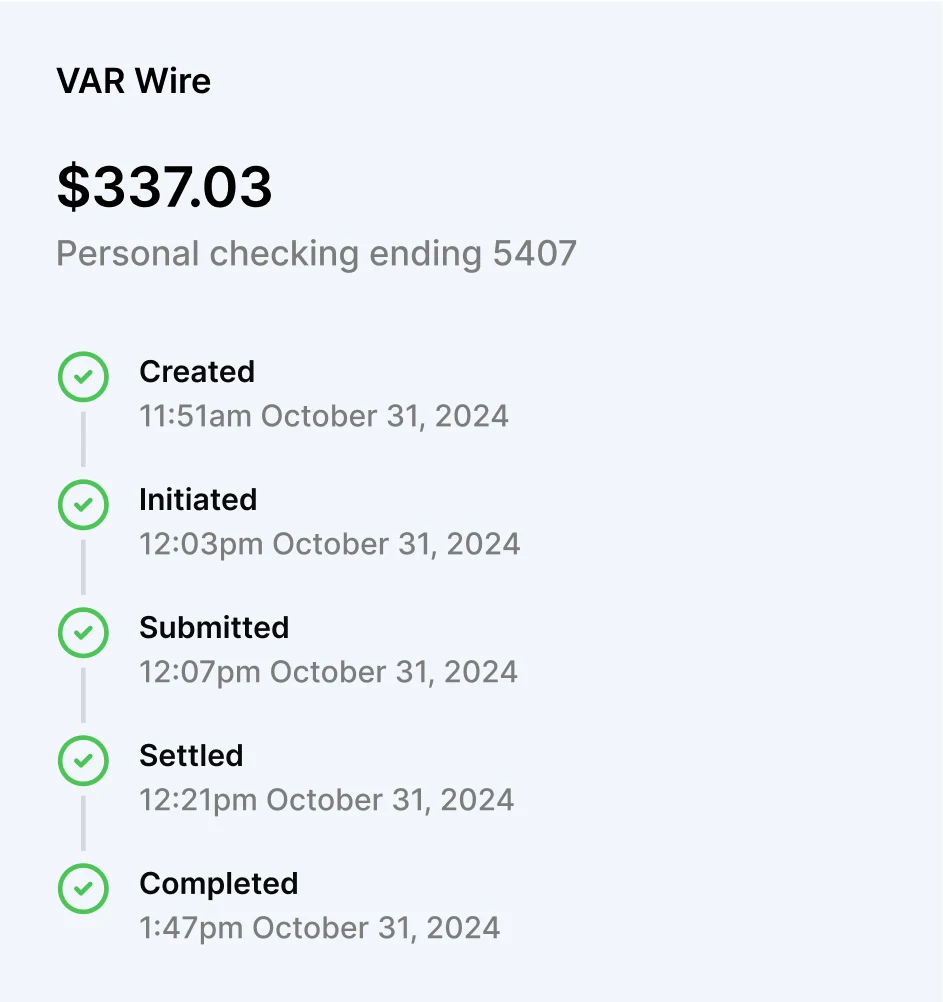
Unparalleled VAR flexibility
VAR has a reputation for taking too long. At Charter, we optimise for the fastest VAR transfers possible — often in a matter of hours.
Unlike legacy banks and middleware providers, we have a direct connection to the Federal Reserve to facilitate the quickest transfers.
Unparalleled VAR flexibility
VAR has a reputation for taking too long. At Charter, we optimise for the fastest VAR transfers possible — often in a matter of hours.
Unparalleled VAR flexibility
Unlike traditional banks and middleware, we connect directly with the Federal Reserve to ensure the fastest, most transparent transfers possible.